Ab und Aufzug
Hans, Wilhelm, and Klaus are three business tycoons in a three-story skyscraper with one elevator. We know in advance that they will call the elevator simultaneously after their meetings tomorrow and we want to get them to their destinations as quickly as possible (time is money!). We also know that the elevator will be on the first floor when they call it. We're going to use search to find the best path for the elevator to take.
- Hans starts on the 2nd floor, and wants to go to the 1st floor.
- Wilhelm starts on the 3rd floor, and wants to go to the 1st floor.
- Klaus starts on the 3rd floor, and wants to go to the 2nd floor.
State will be stored as a tuple whose first element is the location of the elevator and whose second element is a tuple with the locations of Hans, Wilhelm, and Klaus, in that order. A location of None means that the person in question is riding the elevator. So the state (2, (None, 1, 2)) means that Hans is on the elevator (which is on the 2nd floor), and Klaus is on the 2nd floor as well (but not on the elevator), whereas Wilhelm is on the 1st floor.
From any state, the child states are generated by trying the following, in order:
- ED: the elevator moves down one floor
- EU: the elevator moves up one floor
- 0On: Hans gets on the elevator
- 0Off: Hans gets off the elevator
- 1On: Wilhelm gets on the elevator
- 1Off: Wilhelm gets off the elevator
- 2On: Klaus gets on the elevator
- 2Off: Klaus gets off the elevator
Let's say it takes one minute for the elevator to move one floor in either direction, and it takes one minute for anyone to get on or off the elevator unless Klaus is involved. It takes Klaus five minutes to get on or off the elevator (he's extremely slow); it also takes everyone else five minutes to get on or off the elevator if Klaus is already riding the elevator (he's also extremely talkative).
Goal
Write the goal function, which should make sure that everyone is on the right floor, and no one is on the elevator.
Search Strategies
Suppose that we are in the middle of the search and the search agenda consists of the following nodes (listed in the order that they were added to the agenda, earliest first):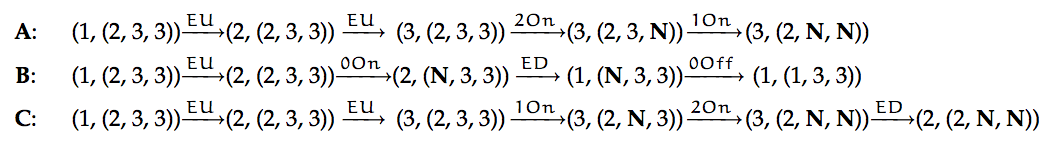
- Assume that no states other than the ones listed were visited in the search.
- An illegal action leaves you in the same state and Pruning Rule 1 applies (don't consider any path that visits the same state twice).
- Assume that the order of operations is as listed at the beginning of this problem: ED, EU, 0On, 0Off, 1On, 1Off, 2On, 2Off
Note that in general you may have to expand more than one node to find the next state that is visited.
When entering states, use None, 1, 2 or 3; do not use N.
BFS
If we are using breadth-first search without dynamic programming, but with pruning strategy 1 (don't consider paths that visit the same state more than once):
DFS
If we are using depth-first search without dynamic programming, but with pruning strategy 1 (don't consider paths that visit the same state more than once):
BFS+DP
If we are using breadth-first search with dynamic programming:
UC
If we are using uniform-cost search with dynamic programming:
Heuristics
Frieda, Lola, Ulrike, and Xenia (four engineers) are asked to produce heuristics to speed up the search. In all the heuristics, distance is measured in number of floors.- Frieda suggests a heuristic F: the maximum of the distances between each person and his destination plus 2 times the number of people who are not on the right floor.
- Lola suggests a heuristic L: the maximum of the distances between each person and his destination plus 10 if Klaus is not on the elevator and not on the right floor, plus 5 if Klaus is on the elevator.
- Ulrike suggests a heuristic U: the sum of the distances between each person and his destination.
- Xenia suggests a heuristic X: the maximum of the distances between each person and his destination
Which of these heuristics are admissible for this problem? Enter some
combination of the letters F, L, U, and X
below, with no punctuation: