Searchy

Consider the following graph:

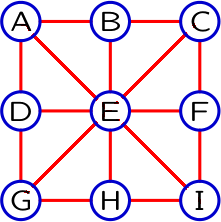
• the start state is A
• the goal state is I
• children are pushed onto the agenda in reverse alphabetical order. The first three paths pushed onto the agenda after A (our initial path) are AE, AD, and AB, in that order. Notice that, depending on whether we are running BFS or DFS, the order in which paths are popped off the agenda will be different.

Enter any paths as a sequence of state names, with no punctuation, e.g. ABCD

What is the final path found by a breadth-first search?

Which of the following is guaranteed to be true about the shortest path between any two arbitrary states in the graph above?
-- The path includes state E The path includes at most three states The path includes at least three states