A Little Something Refreshing
Ben Bitdiddle decides to undertake an experiment in evolutionary biology, to see how the food preferences of a species evolve over time. He knows (as anyone who studies biology knows) that all turtles prefer one of three foods: grapes, lettuce, or hamburgers.
Assume that all of the turtles in a given generation share the same favorite food. We will represent the n^{\text{th}} generation's favorite food as a random variable F_n. Through much careful study, you determine that F_n's evolution is governed by the following Markov model, where arrows represent generational transitions:
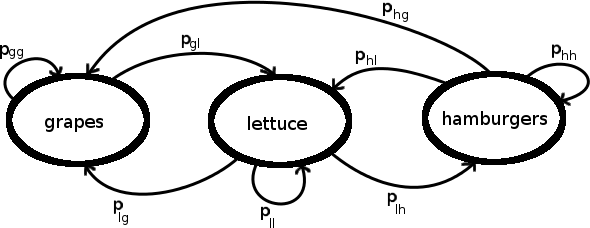
The transition probabilities are given as follows:
- p_{hh} = 0.6
- p_{hl} = 0.3
- p_{hg} = 0.1
- p_{lh} = 0.3
- p_{ll} = 0.5
- p_{lg} = 0.2
- p_{gl} = 0.6
- p_{gg} = 0.4
Enter all your answers as decimal numbers, accurate to three decimal places.
Short-term Behavior
Deterministic Start
In this experiment, Ben starts with a generation of turtles that are known to prefer grapes.
If we know that F_0 is grapes, what is the probability that F_1 is lettuce?
If we know that F_0 is grapes, what is the probability that F_2 is lettuce?
Random Start
In this experiment, Ben starts with a generation of turtles with unknown food preference. He assumes that this initial generation's preference is uniformly distributed across the three possibilities.
If F_0 is uniformly distributed across all possibilities, what is the probability that F_1 is lettuce?
If F_0 is uniformly distributed across all possibilities, what is the probability that F_2 is lettuce?
If F_0 is uniformly distributed across all possibilities, what is the probability that F_2 is hamburgers?
Long-term Behavior
After infinitely-many generations, we pick a random turtle and observe its eating habits. What is the probability distribution over this turtle's favorite food?
\lim_{n\rightarrow \infty} \Pr(F_n = \text{grapes}):
\lim_{n\rightarrow \infty} \Pr(F_n = \text{lettuce}):
\lim_{n\rightarrow \infty} \Pr(F_n = \text{hamburgers}):