U Can Also Touch This.
In the previous problem, we looked at how two overlapping, orthogonal resistive sheets can encode the location of touch in an x-y plane.
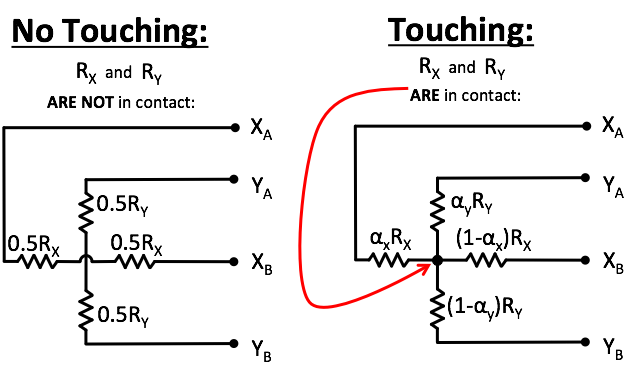
As a refresher, the animated gif below depicts several touch-point events on a 800x600 pixel display encoded with an $R_X = 400k\Omega$ and $R_Y = 200k\Omega$.
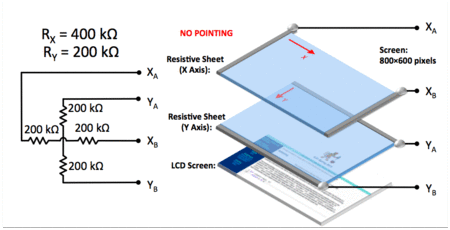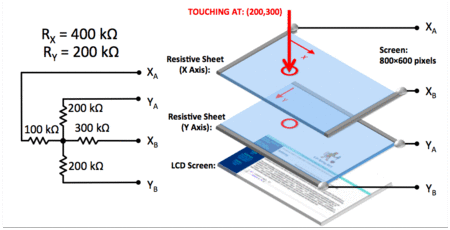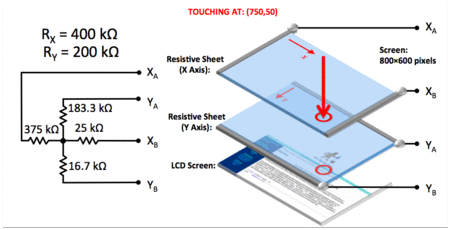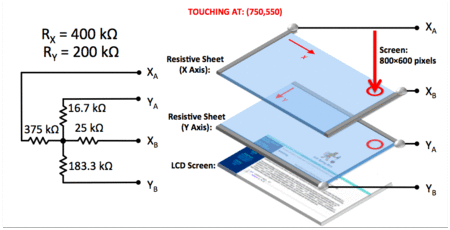
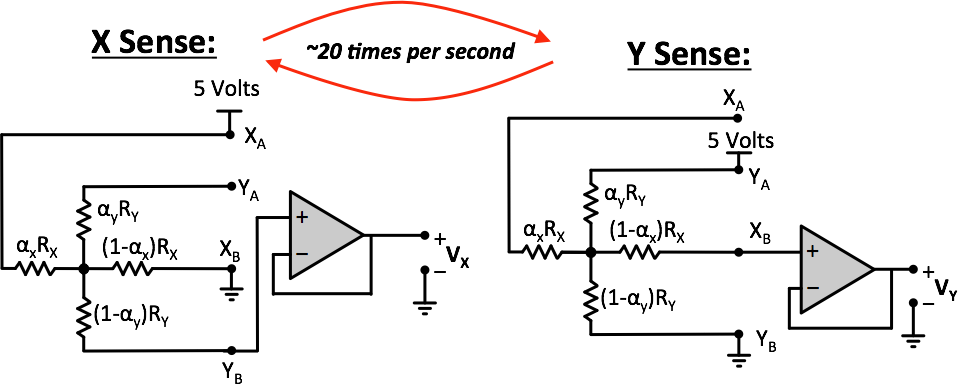
While we can easily calculate the resistances by hand, we still need a way to convert these changes in resistance into meaningful changes in voltage that can then be fed into the necessary electronics for processing. There are several ways to do this. We'll do a simple one here:
- Using switching electronics (which we can ignore) X_A, X_B, Y_A, and Y_B are rapidly switched between two different configurations many times per second (much faster than a potential finger or stylus movement).
- In the first configuration "X Sense", an x-encoding voltage V_X is generated. (Y_A is left unused).
- In the second configuration, "Y Sense", a y-encoding voltage V_Y is generated. (X_A is left unused).
- V_X and V_Y are then used to determine the location of pointing on the screen.
Fill in the table below for a touch screen of 1280 by 768 pixels (x by y dimensions) with resistors:
- R_X = 90.0 k\Omega
- R_Y = 70.0 k\Omega
Enter V_X and V_Y in Volts to two decimal places and enter pixels in integer tuples (example: (100,100))
|
|
|
|
|
| ||
|
| ||
|
|
|