U Can Touch This.

The questions below are due on Tuesday April 02, 2019; 11:00:00 PM.
 
music for this problem

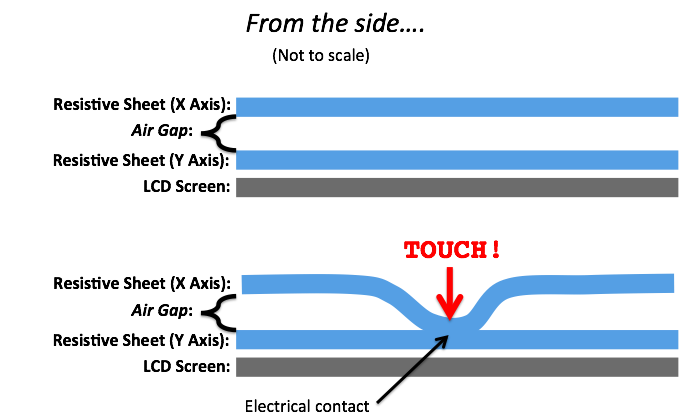
While most touch screens on consumer electronics (tablet computers, smartphones, etc...) use a capacitive technology to detect pointing, cheaper devices and certain niche applications utilize resistive touch screens. Resistive touchscreens are comprised of two separate orthogonal resistive sheets made of a transparent resistive material superimposed above the LCD display as shown in the exploded drawing below:

The two resistive sheets remain electrically isolated from one another until a force (from a finger or stylus) is applied causing the sheets to make electrical contact:

When there is no contact, the system can be modeled as two independent resistors, R_X and R_Y which cross over each other. We are more interested when there something is touching the screen, though. In that case, when there is touching, the system is now represented by two connected criss-crossing voltage dividers. Just like with the potentiometers we've used in class so far, the position along each axis can be represented by an \alpha parameter, with \alpha _X for the X axis and \alpha _Y for the Y axis. It is important to realize that the \alpha parameters are normalized x and y values, that is: the \alpha values change with where the screen is touched. For example:

• Touching directly in the center of the screen will cause $\alpha _X=\alpha _Y=0.5$
• Touching halfway down on the left side of the tablet will make $\alpha _X=0$ and $\alpha _Y=0.5$

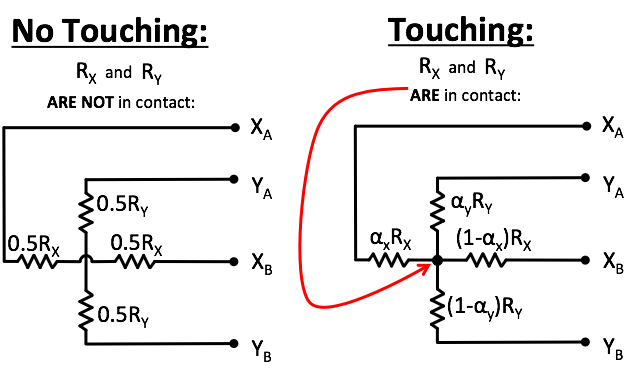
When in contact, two resistive sheets act like overlapping potentiometers that vary based on the x,y coordinates of the contact point. Let's assume we have a mediocre tablet computer with a screen resolution of 1280 by 768 pixels (x by y dimensions) whose spatial coordinates are encoded by the two resistive sheets listed below:

• R_X with a value of 60.0 k\Omega
• R_Y with a value of 30.0 k\Omega

Fill in missing information below that corresponds to the described tablet. Enter data as tuples in the case of alpha parameters or pixels, and in k\Omega in the case of resistances. All values should be entered to two decimal places, with the exception of pixels which can be integers.

1) Part 1

Consider the case when the contact point $(x,y)$, in pixels, is at $(300, 300)$. What are the following values?

2) Part 2

Now consider the case where the contact occurs such that (\alpha_X, \alpha_Y) = (0.547,0.911). What are the following values?