Optimization

Error on line 14 of Python tag (line 15 of source):
    from lib601.sf import SystemFunctional

ModuleNotFoundError: No module named 'lib601'

As we saw with the wall finder system (week 2) and wall follower system (week 3), performance of a feedback control system depends critically on gain. In this exercise, we will develop a framework for choosing gains "optimally."

1) Dependence of Performance on Gain

Our goal is to develop tools to choose parameters of a system that optimize performance. To make this process concrete, we will develop these tools in the context of the following system, which is similar to the wall-finder system from Design Lab 2, but with the time step T=1 second.

1.1) Dependence of Poles on Gain

Write a function make_system_model that takes a gain K as input and returns an instance of System to describe the example system above with that gain. Write your code in optimize.py and debug with IDLE.

Error on line 19 of question tag.
    {'check_function':check_sf,'code':'''s = make_system_model(%f)\nans=(s.numerator.coeffs, s.denominator.coeffs)''' % cs_random.uniform(0,5)},

NameError: name 'check_sf' is not defined

Now use your make_system_model procedure to calculate the poles that result for K=0.01, 0.25, 1, and 2.

Enter the poles you calculated for the system with the following values of K, as a Python list of (possibly complex) numbers.

Error on line 5 of question tag.
    csq_check_function=checker

NameError: name 'checker' is not defined

Error on line 5 of question tag.
    csq_check_function=checker

NameError: name 'checker' is not defined

Error on line 5 of question tag.
    csq_check_function=checker

NameError: name 'checker' is not defined

Error on line 5 of question tag.
    csq_check_function=checker

NameError: name 'checker' is not defined

1.2) Dependence of Unit Sample Response on Gain

We wish to characterize performance by calculating figures of merit based on the system's unit sample response.

The SystemSimulator class can be used to create simulators for any system. This simulator representation will allow us to determine the output of the system for arbitrary input. If we had a System instance called x, for example, we could make a simulator for that system with: sim = SystemSimulator(x). Then we could find the system's response to a particular input by calling its get_response method (see the documentation for more details).

Calculate the unit-sample responses that correspond to the gains in Section.1. Plot your results, and save the plots. We have included code in optimize so that you can generate a plot of the values in the list ylist by calling the stem_plot function:

> stem_plot(ylist)

> idle3 -n &

For each of the gains below, enter a Python list containing the first 10 samples of the unit sample response of the resulting system (n=0 to n=9), assuming the system starts at rest:

Error on line 4 of question tag.
    csq_check_function=list_checker

NameError: name 'list_checker' is not defined

Error on line 4 of question tag.
    csq_check_function=list_checker

NameError: name 'list_checker' is not defined

Error on line 4 of question tag.
    csq_check_function=list_checker

NameError: name 'list_checker' is not defined

Error on line 4 of question tag.
    csq_check_function=list_checker

NameError: name 'list_checker' is not defined

2) Figures of Merit

To develop more quantitative figures of merit, we have provided code that lets you directly compare pole locations and unit-sample responses. This code uses your procedure make_system_model (to determine pole locations and corresponding unit sample response). You can invoke the viewer by running view_root_locus(), which will produce the following window

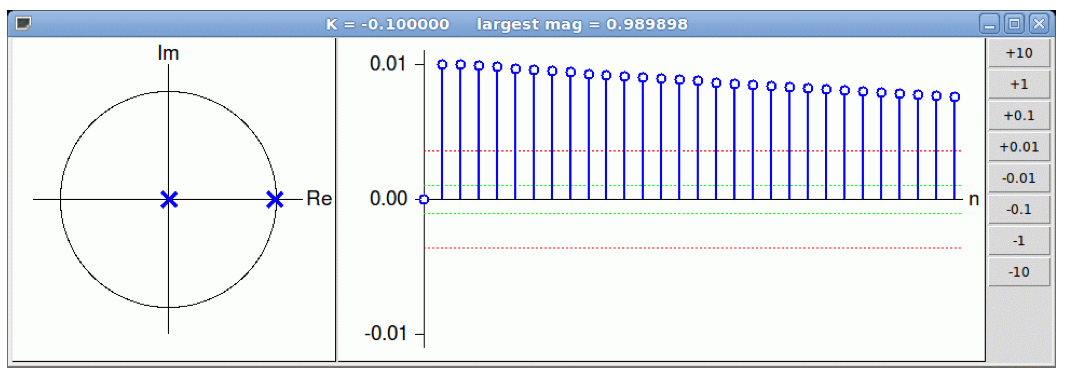
where the poles are shown as complex numbers on the left, the unit sample response is shown in the center, and a column of buttons on the right allow you to increase or decrease the value of K. The scales indicate the maximum values in the plot. The red and green dotted lines indicate the maximum divided by e and 10, respectively.

2.1) Optimality

Use the viewer to determine the following five "optimal" values of K:

K_m: the maximum K for which the response decays monotonically (after n=2).

K_m =~

K_{10}: the maximum K for which the magnitude of the peak negative response (i.e., the "overshoot") is smaller than 10% of the peak positive response.

K_{10} =~

K_e: the maximum K for which the overshoot is smaller than the peak response divided by e.

K_e =~

K_s: the minimum (positive) K for which the response does not converge to zero.

K_s =~

K_d: the K for which the bounding geometric sequence converges fastest.

K_d =~

2.2) Definitions

Which (if any) of the previous definitions of "optimum" K corresponds to the minimum (positive) gain for which some poles are not inside the unit circle?
-- K_m K_10 K_e K_s K_d

Which (if any) of the previous definitions of "optimum" K corresponds to the gain that minimizes the magnitude of the dominant pole?
-- K_m K_10 K_e K_s K_d

Which (if any) of the previous definitions of "optimum" K corresponds to the maximum gain for which all poles are positive and real-valued?
-- K_m K_10 K_e K_s K_d

3) Optimization

We wish to automate the procedure of finding the "optimal" gain. As we saw in the previous section, there are many ways to define "optimal." In this section, we will focus on finding K_d because the underlying metric (i.e., the bounding geometric sequence that converges fastest) is both easy to calculate and useful in a variety of applications. The following plot shows how the magnitude of the dominant pole depends on K for the system in Section 1.

K_d is the value of K that corresponds to the minimum magnitude (here K_d=1/4). In this section, we will explore two methods for finding K_d for arbitrary systems. Since K_d is the minimum of a function, we will look at finding minima of arbitrary functions numerically.

We will consider two different strategies for optimizing functions, and we will compare their performance in different scenarios.

3.1) Linear Optimization

Let's say we want to find, for some function f, the value x such that f(x) is minimized. We will concern ourselves with finding x accurate to within some threshold.

One strategy for doing this is to compute f(a) for a number of values of a, within some specified range. We can start with a equal to the lower bound of the range we are checking, and then increment a by the specified threshold until a is no longer in the specified range. We can compute f(a) for each of these values, and then look through the results for the value that minimized f(a).

Write a procedure called minimum_linear to implement this strategy. Your procedure should take the following inputs:

and should return a tuple (xBest,fBest), where xBest represents the value of x for which f(x) is smallest, and fBest represents f(xBest). xBest should be within threshold of the x value where the true minimum occurs.

As a test, use your minimum_linear procedure to find K_d for the problem in Section 2

Paste your definition for the minimum_linear procedure below. Do not include import statements.

Error on line 22 of question tag.
    {'code':'ans = minimum_linear(lambda x: (x-2)**2, -3, 3, .01)','check_function':make_checker(2,.01)},

NameError: name 'make_checker' is not defined

3.2) Bisection

Notice that the minimum of the function separates regions where the slope of the function is negative (here K\lt 1/4) from regions where the slope is positive (K \gt 1/4). This change in the sign of the slope is a very general property of minima (or maxima) of a function. We can take advantage of the changing sign property to automatically find the minimum of a function (say f(x)) as follows. Assume that we are given a small value of x (say x_0) for which the derivative f'(x) is negative and a large value of x (say x_1) for which the derivative f'(x) is positive. If f(x) is a "smooth" function of x and if it has a single minimum value, then the minimum occurs for x_0 \lt x \lt x_1. We can halve this range as follows:

1. Define the midpoint x_2={1\over 2}(x_0+x_1).
2. Calculate f'(x_2).

Now if f'(x_2)\lt0, we know that the minimum occurs for x_2\lt x\lt x_1. Alternatively, if f'(x_2)\gt0 we know that the minimum occurs for x_0\lt x\lt x_2. In either case, we have halved the interval. We can repeat this procedure to determine the location of the minimum to arbitrary precision. This method, which is called bisection, is an example of "divide-and-conquer."

Write a procedure called minimum_bisection to implement the bisection method. Your procedure should take the following inputs:

and should return a tuple (xBest,fBest), where xBest represents the value of x for which f(x) is smallest, and fBest represents f(xBest). xBest should be within threshold of the x value where the true minimum occurs.

Hint: We can use the procedure to evaluate f(x) to approximate the slope at x numerically, e.g.,

where \delta represents a small number, say 10^{-6}.

As a test, use your minimum_bisection procedure to find K_d for the problem in Section 2

Paste your definition for the minimum_bisection procedure below. Do not include import statements.

Error on line 22 of question tag.
    {'code':'ans = minimum_bisection(lambda x: (x-2)**2, -10, 10, 1e-6)','check_function':make_checker(2,1e-6)},

NameError: name 'make_checker' is not defined

4) Comparison

Answer the following questions comparing minimum_linear and minimum_bisection.

Assume that we make a call to minimum_linear for certain function f over a certain range with a certain threshold and receive a result accurate to within the specified threshold.

If the range were doubled, would we still expect minimum_linear to return a result accurate to within the specified threshold?

-- Yes No

Assume that we make a call to minimum_bisection for certain function f over a certain range with a certain threshold and receive a result accurate to within the specified threshold.

If the range were doubled, would we still expect minimum_bisection to return a result accurate to within the specified threshold?

-- Yes No

Assume that a call to minimum_linear for certain function f over a certain range with a certain threshold calls the function a number of times n.

If the range were doubled, roughly how many times would we expect f to be called?

-- n times n+1 times n+2 times 2*n times n**2 times 2**n times

Assume that a call to minimum_bisection for certain function f over a certain range with a certain threshold computes the derivative of f a number of times m.

If the range were doubled, roughly how many times would we expect the derivative to be computed?

-- m times m+1 times m+2 times 2*m times m**2 times 2**m times

Assume that a call to minimum_linear for certain function f over a certain range with a certain threshold calls the function a number of times n.

If the threshold were decreased by a factor of 100 (e.g., from 1 to .01), roughly how many times would we expect f to be called?

-- n times n+1 times n+7 times 100*n times n**100 times 100**n times

Assume that a call to minimum_bisection for certain function f over a certain range with a certain threshold computes the derivative of f a number of times m.

If the threshold were decreased by a factor of 100 (e.g., from 1 to .01), roughly how many times would we expect the derivative to be computed?

-- m times m+1 times m+7 times 100*m times m**100 times 100**m times