Superposition

The questions below are due on Monday February 18, 2019; 11:00:00 PM.

You are not logged in.
If you are a current student, please Log In for full access to this page.

Recall that the unit sample signal \Delta is defined as:

\delta[n] = \cases{ 1 & if $n=0$\cr 0 & \text{otherwise} }

and that the unit step signal U is defined as:

u[n] = \cases{ 1 & if $n\geq 0$\cr 0 & \text{otherwise} }

The unit sample response of a system is the output of that system when its input is the unit sample signal \Delta, and the unit step response of a system is the output of that system when its input is the unit step signal U

Relationship

Before moving on, note the following relationships:

\Delta = (1 - {\cal R})U

U = \Delta + {\cal R}U

Check Yourself 1:

Prove to yourself that these equations are correct.

Check Yourself 2:

If we knew a system's unit sample response {\cal H}\Delta, how could we use the above equation to determine the system's unit step response {\cal H}U?

Hint: what happens when you apply {\cal H} to both sides of the equations above? Can you arrange them to solve for one response in terms of the other?

Part 1

Consider a system with a unit _sample_ response $h[n]$:

h[n] = \begin{cases} 0 & n \leq 0 \\ 0.5 & n > 0, \text{and}~n~\text{even} \\ -0.5 & n > 0, \text{and}~n~\text{odd} \end{cases}

This response is depicted below:

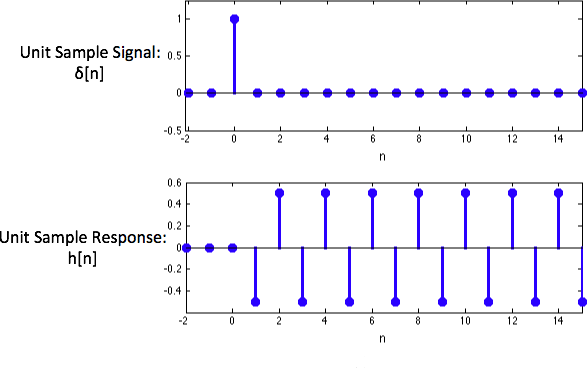
Determine the first six values of this system's unit step response s[n] Enter a Python list of length 6 below, representing [s[0], s[1], s[2], s[3], s[4], s[5]].

First 6 samples of unit step response:

Part 2

Consider a system with a unit _step_ response $s[n]$:

s[n] = \begin{cases} 0 & n \lt 0 \\ 1 & n = 0 \\ 3 & n > 0 \end{cases}

This response is depicted below:

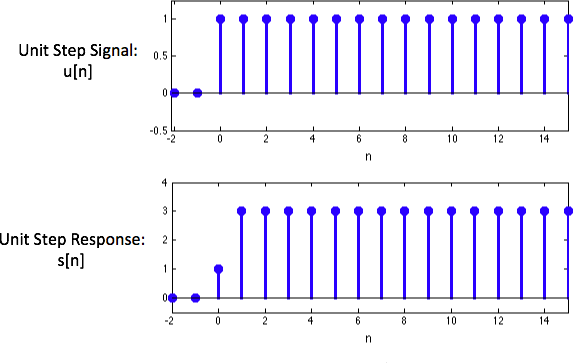
Determine the first six values of this system's unit sample response h[n]. Enter a Python list of length 6 below, representing [h[0], h[1], h[2], h[3], h[4], h[5]].

First 6 samples of unit sample response: