Design Lab 13: When You Wish Upon A*
Files
This lab description is available as a PDF file here. Code is available here, or by running `athrun 6.01 getFiles`.1) Getting Started
Do this lab with your assigned partner. You and your partner will need a lab laptop, or you may use your personal machine, provided you have installed the lib601 software. Get today's files by running:
athrun 6.01 getFiles
or from the link above.
2) Preparation
Last week, we used remarkably concise search algorithms to find paths through complicated mazes. Today we will use slight variations of those search algorithms to solve an even larger problem: planning routes for driving across the USA.
This lab will make use of publicly-available highway data from the U.S. Federal Highway Administration1.
Our Python representation for these data consists of two main classes (defined in highways.py and imported into designLab13.py):
- Location: An instance of this class represents a single point on a map. Each instance includes a unique identifier id_number, and latitude and longitude coordinates (latitude and longitude, respectively). Instances also contain an attribute name, which contains a (more-or-less) human-readable string identifier. Some locations are not named; for these locations, name will contain None.
- Link: An instance of this class represents a bidirectional highway between two locations. Each instance contains attributes begin and end, which hold instances of Location representing the two ends of the link. Some instances also contain an attribute name, which contains a (more-or-less) human-readable string identifier. In addition, each instance has an attribute max_speed, which contains the maximum speed you are allowed to drive along it.
The following structures and procedures are also defined in highways.py and imported into designLab13.py:
- location\_from\_id: a dictionary that maps each location's unique id number to the corresponding instance of Location
- location\_from\_name: a dictionary that maps the name of a location to the corresponding instance of Location
- links: a list containing each Link in the database.
- distance(loc1, loc2): a function that takes two ID numbers and returns an estimate of the distance between the locations they represent, in miles, incorporating an approximation for the curvature of the earth. This will serve as our cost function.
- locations\_matching\_name(state, name): a method that takes two strings as input, and returns the names and ids of matching locations as a list of tuples. For example, locations\_matching\_name('IL','PRINCETON') returns [('ILPRINCETON C-N', 17001075), ('ILPRINCETON E', 17001089), ('ILPRINCETON', 17001088)].
2.1) Helpers
To find routes through these maps, it will be convenient to know which locations are neighbors (i.e., which Locations are connected by single Links). Since locating neighbors is slow, we will find the neighbors once, and record them in a dictionary.
Open the file designLab13.py and complete the definition of the procedure make_neighbors_dict, which takes no arguments and returns a dictionary that maps each location's unique ID number to a list of ID numbers corresponding to its neighbors.
Eventually, we will also want an easy way to compute the total cost of a path. Write a function path_cost that takes a list of id numbers as input, and returns the total cost of that path in miles (the sum of the distances between locations). A skeleton has been provided in designLab13.py.
2.2) Representation
Use the methods and variables from designLab13.py and highways.py to answer the following. Decimal answers must be accurate to four decimal places.
Scale
Data
[17001088, 17001089, 17001106, 17001147, 17001168]
3) Search
Now we want to use the search procedures we developed over the last couple of weeks to find paths in the map. As usual, we will need to implement a successor function to specify this search domain.
What is a good representation for state in this search problem?
How would you implement your successors function, given this representation?
Implement the highway_successors function.
As a test, we will use search to run a BFS to find a path from a place near the geographic center of the U.S. (Smith Center, KS; ID number 20000071), to Cambridge (ID number 25000502).
Make a note of the number of states in the path found by BFS, and also of the total cost of the path found.
3.1) Uniform Cost
Now we will update our code to use uniform cost search (which is implemented as a function uc_search in designLab13.py). Note that this function is different from the one in SL13, as it only returns the path, rather than a (path, cost) tuple.
Since UC search is trying to find the path with smallest cost, we will need to represent the cost of the links in our successor function. We will do this by making our successor function to return tuples of the form (state, cost).
Define a new successor function for use with uc_search, or modify your old successor function so that it can be used with uc_search..
As a test, use uc_search to find a path between Smith Center, KS, and Cambridge, MA (the same two locations we just tested with BFS).
Please answer the following questions about the path you found from 20000071 to 25000502. Decimal answers must be accurate to one decimal place.
3.2) Viewing Your Paths
Looking at lists of ID numbers isn't very informative. As an alternative, we can view our paths on a map to get an idea of how good the results are.
highways.py contains a function print_kml(path) which takes a list of node IDs as input and prints a KML string, as well as a function save_kml(path, filename), which saves the corresponding KML string in a file.
You can view your path by copying/pasting the KML string into:
http://display-kml.appspot.com/
Use the above tool to visualize your BFS and UC paths. We'll discuss them during the checkoff.
Discuss your results with a staff member. How do the paths returned by BFS and UC Search differ? Why is this?
4) Evaluation
We will now try running uniform cost search in a few different trials to try to get a feel for how it performs in different circumstances. In order to understand and measure the performance of uc_search, you are free to modify or augment the implementation provided in designLab13.py.
4.1) Specifics
Run your search through the following scenarios, and make note of the total cost of the path found, as well as the number of states expanded, in each case.
- Find a path from Pittsfield, MA (ID 25000379) to Cambridge (25000502), without a heuristic.
- Find a path from Altoona, PA (ID 42001780) to Cambridge, without a heuristic.
- Find a path from Smith Center, KS (ID 20000071) to Cambridge, without a heuristic.
Answer these tutor questions about your results.
Pittsfield, MA (25000379)
How many states were expanded by uniform cost search with no heuristic?
What was the total cost of the path found with no heuristic?
Altoona, PA (42001780)
How many states were expanded by uniform cost search with no heuristic?
What was the total cost of the path found with no heuristic?
Smith Center, KS (20000071)
How many states were expanded by uniform cost search with no heuristic?
What was the total cost of the path found with no heuristic?
4.2) Generalizing
In this section, we will try to find a general trend between the cost of the path returned by a uniform-cost search starting at the center of the US, and the number of states expanded over the course of that search.
Consider the plot below, which shows the number of states expanded over the course of a uniform cost for paths of various lengths (all of which start at Smith Center, KS):
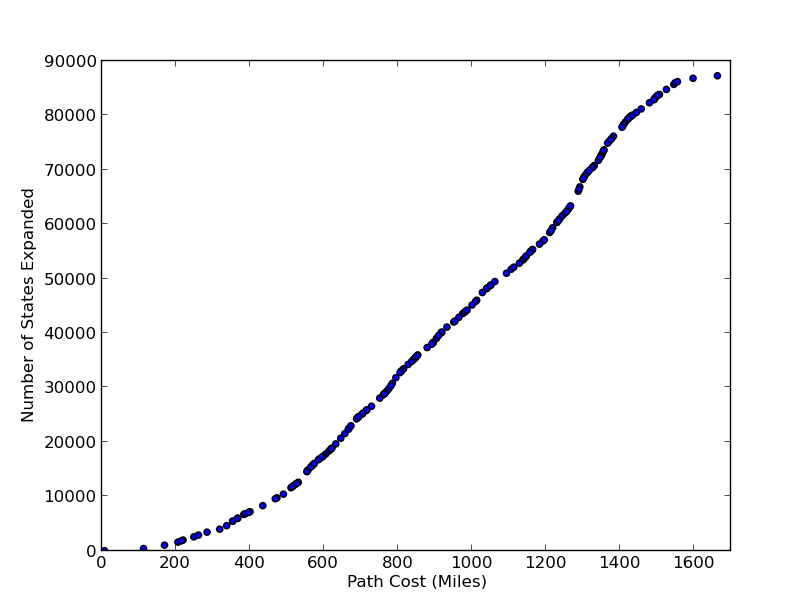
Consider the geometry of the space over which we are searching and the cost function we are using. Does this graph match your expectations? Explain the relationship between the number of states expanded and the cost of the final path found.
Why does the graph seem to grow faster than linearly for small paths, then appear to grow linearly, and then remain constant for very long paths?
It may help to note that the height of the contiguous United States (the distance from the northern border to the southern border) is approximately 1500 miles, and that the width of the contiguous Unites States (from east to west) is approximately 2800 miles. How do these numbers manifest in the graph above?
5) Heuristics
In uniform-cost search, we select the next node to expand that minimizes F(n) = path\_cost(n).
In this section, we will consider A* (uniform cost search with a heuristic function), in which we select the node that minimizes F(n) = path\_cost(n) + H(n), where H is a heuristic function that estimates the distance from n to the goal.
Repeat your specific searches from the previous section, this time using the geodesic distance between the current state and the goal (which can be computed with the distance function) as a heuristic.
Pittsfield, MA (25000379)
What fraction of the states expanded with no heuristic are expanded with distance as a heuristic?
Altoona, PA (42001780)
What fraction of the states expanded with no heuristic are expanded with distance as a heuristic?
What was the total cost of the path found with distance as a heuristic?
Smith Center, KS (20000071)
What fraction of the states expanded with no heuristic are expanded with distance as a heuristic?
What was the total cost of the path found with distance as a heuristic?
Discuss your results with a staff member.
6) A Weighty Problem
It is interesting to explore a range of methods that "interpolate" between Uniform Cost Search and A*, and then go beyond A* in terms of how much they are affected by distance to goal.
A weighted version of A* has an additional parameter \alpha that ranges between 0 and 1, and selects the next node to expand by finding the one that minimizes
\alpha =
\alpha =
- costs should be a list containing the cost of the path found from Hollister to Cambridge as \alpha is varied from 0 to 1 (inclusive) with a step size of 0.01 (i.e., costs[0] should be the cost of the path found when \alpha=0.0; costs[1] should be the cost of the path found when \alpha=0.01; etc). Note that costs should be a list of length 101.
- expanded should be a list containing the number of states expanded when searching from Hollister to Cambridge as \alpha is varied form 0 to 1 (inclusive) with a step size of 0.01. Note that expanded should be a list of length 101.
Discuss your results with a staff member.
7) Need for Speed (Limits)
So far, our planning has been based purely on distance, but oftentimes, when planning a route between two locations, we are actually interested in the amount of time it will take to move from one location to another. Modify your highway_successors function (and/or your make_neighbors_dict function) so that they output a cost in terms of time, rather than distance (you may assume that a person can travel at a link's speed limit for the entire length of the link).
Run your updated search (with an effective, admissible heuristic) to find the minimum time path between Smith Center, KS (20000071) and Cambridge, MA (25000502).
Discuss your results, including your choice of heuristic, with a staff member.
Use the path visualizer to visualize the UC search paths, with distance as cost and with time as cost. What is different about them? How can you explain this difference?
Footnotes