Design Lab 11: In It For the Long Hall

The questions below are due on Thursday April 25, 2019; 09:55:00 PM.
 

Partners: You have not yet been assigned a partner for this lab.

Files

This lab description is available as a PDF file here. Code is available here, or by running athrun 6.01 getFiles.

Music for this Lab

1) Getting Started

You should complete this lab with your assigned partner. You should use a lab laptop for this lab, or another computer running GNU/Linux. This lab does not work reliably on MacOS or Windows.

You will need the code distribution for this lab, which is available from the links above, or by running athrun 6.01 getFiles from a lab machine. You should start by pasting in your transition model from SL11 into localizeBrain.py.

2) Introduction

Earlier this week, we explored Bayesian state estimation in a simple discrete domain by examining how Bayesian updates and transition updates affected our belief about the state of the underlying system. In this lab, we will apply those ideas to estimating the position of the robot in a `soar` simulation. The bulk of the lab will be spent building probabilistic models of the robot's sensing and motion.

We will place the robot at an unknown location in a hallway where the locations of walls are known, and have it drive along a smooth wall on its right using the controller we developed in Design Lab 3. As it drives, we will refine our estimate of the robot's location using sonar readings of the distance to the left wall.

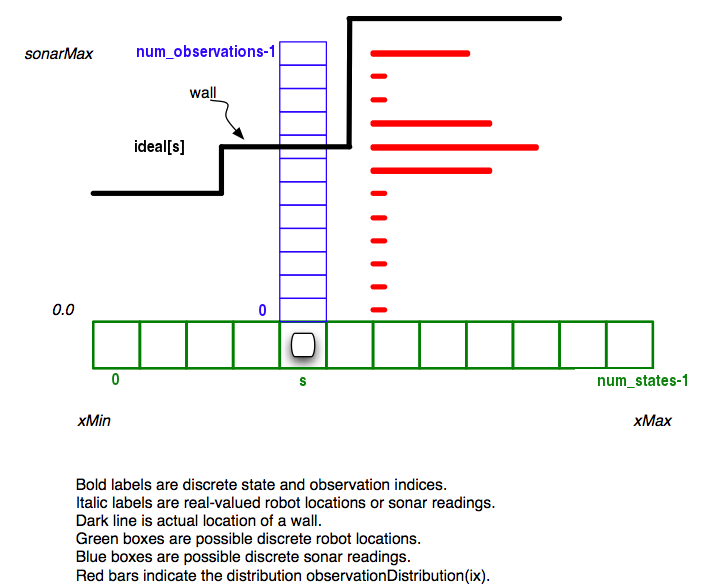
Although the actual robot location and sonar readings have continuous values (in meters), the estimator will represent them with discretized locations (states) and sonar distances (observations), as shown in the figure below, and described by the following:

• States: The robot will only be moving in the x direction, with real-valued coordinates ranging from x_min to x_max. We will discretize that range into num_states equal-sized intervals, and say that when the robot's center is within one of those intervals, then it is in the associated discrete state. The discrete states range from 0 to num_states - 1, inclusive.
• Observations: On each step, the robot will make a distance observation with its leftmost sonar. Valid readings will be floating-point numbers between 0 and sonarMax. We will discretize this range into num_observations equal-sized intervals. The discrete observations range from 0 to num_observations - 1, inclusive. Errors (which are reported by SoaR as 5) are discretized as numObservations - 1.
• Ideal observations: We make a simplifying assumption that all states with the same distance to the left wall will have the same observation distribution; to aid in calculating this, we represent the map using a list called ideal. This list is of length num_states, and it contains, for each state, the distance to the wall on the left, represented as an integer between 0 and num_observations - 1, inclusive.
• Transitions: The robot will move to the right at a constant velocity.

3) Observation Models

We began in software lab by modeling the robot's movement through the world.

In that setup, the robot was working in a very benign environment, moving completely reliably completely parallel to the wall. Now, we'll start the robot at an angle and run a stable-but-oscillatory controller to move it along the hallway¹.

In Soar, open the localizeBrain.py brain in the gapWorldTilt.py world, and run the brain again by stepping. You should set TRANS_MODEL_TO_USE to be your transition model from software lab.

3.1) Correction

In the previous section, we noticed an issue: the robot can sometimes observe something other than the ideal value! In this section, we will try to account for this.

Update the the observation model (defined in obs_model) to be more appropriate for this domain, and change the variable OBS_MODEL_TO_USE to obs_model, so that the state estimation process uses your new observation model.

Make sure your localizer is robust to the granularity of the observations. Try changing the num_observations variable in localizeBrain.py. Make sure your localizer works with num_observations = 3, 60, and 200 when num_states is held constant at 75.

Paste your code for obs_model below.

4) Running

**Note that passing the tutor checks above does not guarantee the success of your localizer.**

Run your code in gapWorldA.py, gapWorldB.py, gapWorldC.py, and gapWorldTilt.py, and make sure it is able to localize in each.

Also try adjusting the robot's starting location to make sure your localizer works reasonably well for a variety of starting conditions. Left-clicking on the robot and dragging will adjust the robot's position, and right-clicking and dragging will adjust the robot's angle.

5) Measuring Success

Eventually, we would like to make the robot park itself, using the state estimation process from above until it is "certain enough" of its position to consider itself localized, and then using that position estimate to park itself.

To begin, we would like to see how each of the pieces developed above affects the state estimation process. In this section, we will run several experiments to see how the transition model and observation model affect the evolution of the belief distribution by looking at a new type of graph.

5.1) Just Transitions

Start by setting the SHOW_BELIEF_MEASURE_PLOT variable to True in localizeBrain.py. With this variable set, the robot will move through the world as before, but an additional plot will be generated when the Stop button is pressed.

For our first trial, use the following parameters, which will use your transition model from above, but an observation model that leads to updates that don't change the belief based on observations:

INIT_DIST_TO_USE = spiked_init_dist
OBS_MODEL_TO_USE = uniform_obs_model
TRANS_MODEL_TO_USE = trans_model

Open `soar` and load the `gapWorldB.py` simulation world. Run the brain **until the robot has moved beyond the right-most of the three walls**, and then click stop (you may find it helpful to "step" through the simulation, but using the "run" button will be a more efficient way to generate the plots). A plot will appear, which we'll call a _belief measure_ plot.

On the horizontal axis is the step number of the execution. On the vertical axis is the total amount of probability assigned by the current belief distribution to discrete states that are within .25m of the true state of the robot²:

5.2) Naive Observation Model

Now, let's return to the previous observation model and initial state

INIT_DIST_TO_USE = uniform_init_dist
OBS_MODEL_TO_USE = naive_obs_model

Click Reload Brain and World, and run the brain again, until the robot moves beyond the right-most wall.

5.3) Your Models

Finally, run the simulation using your transition model and your observation model (after pasting your observation model into this file):

OBS_MODEL_TO_USE = obs_model

Run the simulation one more time, as above.

6) Free Parking

To this point, we have developed probabilistic models to describe the robot's movement through a 1-dimensional hallway, and to characterize our uncertainty about the robot's observations (sonar readings).

Now we will build on this, using the resulting distribution over positions to predict where the robot is and to decide when it is certain enough of its position to execute a parking procedure and arrive at the position shown below.

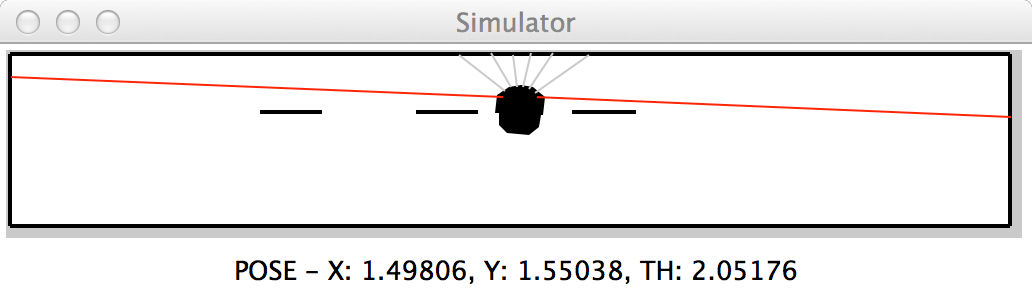
As before, we will place the robot at an unknown location in a hallway where the locations of walls are known, and have it drive along a smooth wall on its right using the controller we developed in Design Lab 4, moving forward at a constant velocity of 0.2 meters per second. As it drives, we will refine our estimate of the robot's location using sonar readings of the distance to the left wall.

7) Deciding When to Park

Now, let's use this belief distribution to do something useful! We will use the belief distribution to decide when the robot is localized well enough to execute a pre-programmed parking maneuver. The final parked state is shown in the first figure of this lab.

It's important to know where you are before you start trying to park (unless you view parking as a contact sport). Imagine that, once it has decided to park, the robot can automatically move backward and park in the appropriate parking space, without losing any positional information.

Now, think about a test on the belief distribution that will guarantee that with some reasonably high probability (e.g. 90 percent) that, if the test is true and the robot parks, it won't run into anything.

You may find it useful to know that the gap between the walls where the robot is supposed to park is 0.75m and the total width of the robot is 0.3m.

Be sure that your criterion is insensitive to the number of states. Currently num_states is set to 100. It should work with num_states = 30 and num_states = 300 as well³.

Edit the confident_location procedure in the brain file. It takes a belief (an instance of dist.DDist) as input and returns a tuple (location, confident) where confident is a boolean value that is True if the robot is certain enough of its location to park and location is an integer state number indicating where the robot thinks it is.

Now, test your robot's parking abilities! When the robot becomes sufficiently certain of its position, you should make it quit running the state estimator and start to park.

To this end, fill in the part of the brain responsible for driving the robot to its final location. It is fine to assume that the robot's movement is perfect (i.e., moving from its estimated location to the parking spot location can be accomplished exactly, using the robot's internal odometry).

Note that this procedure can be carried out as a sequence of steps:

• If the robot is not already lined up with the parking space, drive toward the parking space.
• If the robot is lined up with the parking space but facing in the wrong direction, rotate.
• If the robot is lined up and facing the right direction but is not yet in the parking space, drive forward.

You may consider the robot to have parked when it is 0.3 meters away from the top wall.

Implement your parking procedure, and test your parking robot in gapWorldA, gapWorldB, and gapWorldTilt.py. Your parking procedure should not rely on the 'ground truth' location of the robot, but rather on the estimated position of the robot.

For each of these worlds, run your parking brain with num_states=100 and num_observations=30 until the robot has stopped completely in its designated spot, and then click the "Stop" button in soar.

8) Real Robot

Try your code with a real robot! Find a setup on the side of the room, and log in to that laptop with your Athena account. Do not bring your laptop with you from the table where you were working.

Change REAL_ROBOT to True in parkingBrain.py. Run the brain, and fix any aberrant behaviors that were not apparent in the simulation.

Be sure to "Reload Brain And World" in between trials.

 

---

Footnotes

¹When you're working with the real robot later today, it is not very likely that you will be able to start the robot facing exactly parallel to the wall, or at exactly the right distance away, and so we want to make sure the localizer is robust against small changes in the robot's starting location. (click to return to text)

²Of course, the true state of the robot is not something we can know in a real application; but because we are running in simulation, we can use this ground truth information to gauge how effective the state estimation is. (click to return to text)

³Note that the "run" button will likely not work with num_states set to 300; in that case, you should use the "step" button instead. (click to return to text)