Files

1) Getting Started

You should complete this lab with your assigned partner. You may use any machine that reliably runs soar.

Get today's files by running

$ athrun 6.01 getFiles

2) Introduction

In the software lab, we considered the steps of updating based on an observation (a color reading). Today, we will combine those updates with updates based on transitions (the robot moving).

In software lab, we characterized the robot's observations with an observation model, which told us, given a robot's state, how likely it was to make various observations: \Pr(O=o~|~S=s).

We can also characterize the robot's transitions with a transition model: given the robot's state on timestep t, the distribution over states the robot could be in at time t+1: \Pr(S_{t+1}=s'~|~S_t=s).

Today, we will also put these two pieces together to implement a general-purpose Bayesian State Estimator, which will update a belief based on successive observations and transitions.

2.1) An Abbreviated Hallway

If its observation model is

def obs_given_loc(loc):
    if loc == 0 or loc == 3:
        return DDist({'pink': .8, 'yellow' : .2})
    else:
        return DDist({'pink': .2, 'yellow' : .8})

and its transition model is set such that, on each step, the robot moves one room to the right with probability 0.7, and stays in the same room with probability 0.3 (assume also that attempting to move to the right when in the right-most room will cause the robot to remain in that state with probability 1).

Starting from the belief state shown above, if the robot makes an observation 'yellow', what is its new belief state?

After this observation, the robot moves according to the transition model described in the text above. What is its new belief after moving?

Finally, imagine that the robot makes an observation of 'pink' . What is its new belief state?

3) State Estimator

Error on line 2 of Python tag (line 217 of source):
    from lib601.dist import *

ModuleNotFoundError: No module named 'lib601'

This math can get a little tedious for larger problems, like estimating the robot's position in a longer hallway. As such, we will implement a general-purpose Bayesian state estimator in this section, which we will then use to make estimates about our simulated robot's location, and, eventually, to make estimates about the real robot's position.

We will implement a state estimator by way of a class called StateEstimator. At initialization time, StateEstimator takes three arguments:

• an instance of DDist representing the original distribution over states,
• a function representing the observation model to use (the conditional distribution over observations at time t, given a state at time t), and
• a function representing the transition model to use (the conditional distribution over states at time t+1, given a state at time t).

We will implement two methods in StateEstimator:

• observe(self, obs): updates self.belief based on making an observation obs
• transition(self): updates self.belief based on making a transition

Implement the methods observe and transition in the body of the StateEstimator class in designLab10.py. Each method should update self.belief, but should not return anything.

You may find the documentation for the dist module helpful!

Error on line 78 of question tag.
    ans = se.belief.d''','check_function':output_check},

NameError: name 'output_check' is not defined

3.1) Simulator

You can invoke it by running the following from a terminal window:

$ cd ~/Desktop/6.01_S19/designLab10

$ python3 designLab10.py

or by opening designLab10.py in IDLE and running it, making sure to start IDLE with the -n flag:

$ idle3 -n &

Doing so will create a simulation window:

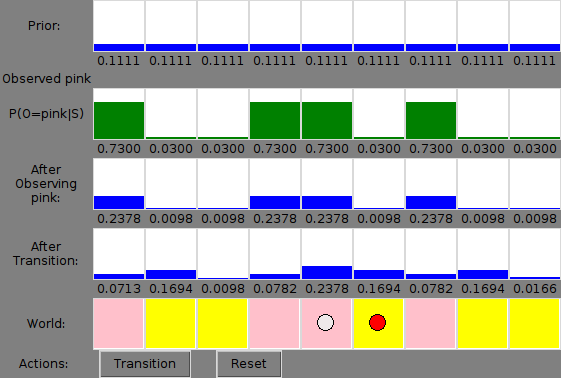
Near the bottom of this window, you will see a display of the world, with a colored box for each state, and a red dot (representing the robot) in one box. Below each box, you see text representing the ideal reading the robot would see if it were in that state and had a perfect sensor. This "world" diagram represents some actual underlying process (in this case, the simulated robot), about which we are making our predictions.

At the bottom of the window, you will see two buttons. Pressing the "Transition" button will cause both the simulated robot and the state estimator to update. Pressing the "Reset" button will cause the simulated robot to return to a new state drawn from the initial distribution, and the state estimator to return to its initial belief state.

After making your first transition, you will see text just below the "prior" belief that tells what sensor reading was observed.

• The first is the prior belief, before updating based on the observation or the action: P(S_ t).
• The second, in green, are the individual probabilities of making the observation we made, for each of the states: P(O|S).
• The third is the belief after updating based on the observation only: P(S'_{t}~|~O_t=o) .
• The final graph is the belief after updating based on both the transition and the observation, P(S_{t+1}). The next time the system is stepped, this distribution will show up as the prior.

The simulator is created by calling the simulate function in designLab10.py. Notice that, as the code is written, the simulator is called with an observation model which always returns the ideal value, and a transition model in which the robot moves exactly one state forward (to the right) on each timestep.

If you change this call to simulate (including changing the models), you will need to close the currently-open simulator window and run the commands above to re-open the simulator.

Check Yourself 1:

Run a few steps of the simulator, and make sure the visualization makes sense. If it doesn't, ask a staff member for help.

Check Yourself 2:

Paste in your observation models from Software Lab 9 (obs_model_A, obs_model_B) and run the simulator with these models. Note that the arguments to StateEstimator control the state estimation process, and the arguments to ColorSimulator control the "ground truth" movements and observations of the simulated robot.

What effect does changing these models have on the way the belief state evolves? Why?

Check Yourself 3:

Also try using transition_model_1 and transition_model_2 instead of move_right_model. How do these models predict the robot will move? What effect does this have on the state estimation process?

Checkoff 1:

Discuss the following with a staff member:

• What is the difference between a state and an observation?
• Explain the `ideal` list.
• What is an observation model, and how is it used in state estimation?
• What is a transition model, and how is it used in state estimation?
• How do `transition_model_1` and `transition_model_2` predict the robot will move?
• Explain the graphs in the simulator window.

4) Different Sensors

Imagine that Chris and Dana both designed color sensors for this robot.

• Chris makes a bad decision when desiging a sensor circuit, so that when the robot is in a room whose actual color is pink, the sensor is guaranteed to see yellow instead (and vice versa). It is entirely reliable (there is no noise), and in rooms with colors other than yellow or pink, it always senses the correct color.

• Dana makes a terrible implementation mistake when building a sensor circuit, leaving values floating, so that when the robot is in a pink or yellow room, it senses pink with probability 0.5, or yellow with probability 0.5, regardless of whether the room is actually yellow or pink. It is able to perfectly sense all other colors.

If we want to use these sensors to help the robot localize itself within the hallways, we need to create observation models that describe their behavior. Create observation models obs_model_C and obs_model_D to characterize Chris's and Dana's sensors, respectively. You may assume that you are provided a dictionary called ideal, which maps a room number to the color of that room.

def obs_model_C(state): pass # your code here def obs_model_D(state): pass # your code here

True or False: Chris's physical sensor used with observation model C behaves equivalently to a perfect sensor with a perfect sensor model.
-- True False

True or False: In an environment with only pink and yellow rooms, Dana's physical sensor used with observation model D behaves equivalently to a perfect sensor with a perfect sensor model.
-- True False

True or False: Chris's physical sensor used with observation model C behaves equivalently to a broken sensor that always returns "NO VALID COLOR" and a sensor model that assigns probability 1 to getting observation "NO VALID COLOR".
-- True False

True or False: In an environment with only pink and yellow rooms, Dana's physical sensor used with observation model D behaves equivalently to a broken sensor that always senses "NO VALID COLOR" and a sensor model that assigns probability 1 to getting observation "NO VALID COLOR".
-- True False

True or False: In an environment with only pink and blue rooms, Dana's physical sensor used with observation model D behaves equivalently to a broken sensor that always returns "NO VALID COLOR" and a sensor model that assigns probability 1 to getting observation "NO VALID COLOR".
-- True False

True or False: In an environment with only pink and blue rooms, Dana's physical sensor used with observation model D behaves equivalently to Chris's sensor and observation model C.
-- True False

Checkoff 2:
Discuss the questions above with a staff member.

5) Hello From the Other Side

So far, we have been thinking about a theoretical robot with a color sensor in a known hallway. However, we would eventually like to use the ideas we have developed so far to help our real robot localize itself in an environment. Our real robot doesn't have a color sensor, so we will not be able to use our work so far exactly, but we can do something similar: rather than sensing colors, though, our robot can sense distances; so we will use the robot's sonar readings as our observations.

The main idea is similar to what we have used so far:

We discretize the robot's x position, and represent it as an integer value between 0 and a constant num_states - 1, inclusive. This integer will be the state of our system. Just like before, although we cannot observe the robot's state directly, we can make observations that are related to the robot's state and use those (along with our initial belief and information about the robot's motion) to estimate the state.

Assume that:

• The robot starts out knowing how many states there are but not knowing what state it is in.
• The robot will observe a discretized sonar value, in the range 0 to 9, representing the distance to the left wall (which depends on the state). The robot knows, for each state, what an ideal distance sensor would read (i.e., it knows the layout of the world).
• The robot will never move backward. If it tries to move past the end of the hallway, it will stay in the forward-most location.

The ultimate goal is for the robot to use its observations, as well as what it knows about the structure of the hallway, to determine its location.

ideal = [5, 7, 6, 4]

Elliot designs a sensor for the robot, but makes a mistake, so that the sensor always returns 9-i, where i is the value that an ideal sensor would read, and then defines the following observation model based on it:

def obs_model_E(loc):
    return DDist({9 - ideal[loc]: 1.0})

Check Yourself 4:

How does the performance of Elliot's sensor (with observation model E) in a world with only ideal values 1 and 8 compare against:

• Chris's sensor with observation model C in a world with only ideal values yellow and pink?
• An ideal sensor (with matching observation model)?
• A broken sensor that always returns 0 (with matching observation model)?

Check Yourself 5:

How does the performance of Elliot's sensor (with observation model E) in a world with only ideal values 2 and 8 compare against:

• Chris's sensor with observation model C in a world with only ideal values yellow and pink?
• An ideal sensor (with matching observation model)?
• A broken sensor that always returns 0 (with matching observation model)?

Check Yourself 6:

How does your ideal observation model need to change in this domain?

Checkoff 3:
Demonstrate your working simulation to a staff member and discuss. How is the state estimation process different now that we are using discrete distances as observations, instead of colors?