Files

Theme song for this lab can be found here.

Do this lab with your assigned partner. You may use a lab laptop, or you may use your own laptop, provided you have installed the 6.01 software.

Get this week's files by running

$ athrun 6.01 getFiles

1) Seeing the light

The robot head has a pair of photodetectors to provide sensitivity to infrared light. The photodetectors are mounted on a printed circuit card that is turned by the motor. When the head is looking forward, the left eye points 45^\circ to the left and the right eye points 45^\circ to the right. The photodetectors are connected through a gray cable from the eye board to the neck board, where they are connected (along with motor and motor pot signals) through a red cable to an 8-pin connector:

When there is a sufficient voltage drop across a photodetector, it can be modeled as a current source that generates a current proportional to the amount of infrared light that strikes it¹; we will use this model throughout today's lab. Throughout this lab, we will refer to the current generated by the left "eye" as I_L, and the current generated by the right "eye" as I_R.

Check Yourself 1:

If I_{photo} is measured in Amps and V_o is measured in Volts, what are the units of the gain c?

Complete the circuit diagram below to design this circuit, including the values of any components you use:

Ultimately, we would like to make two voltages: one proportional to I_L, and one proportional to I_R. In the handout, draw a schematic diagram for two photodetector circuits: one to generate a voltage V_L from the left photodetector, and one to generate a voltage V_R from the right photodetector, using pins 4, 5, and 6 on the head connector. Label V_L and V_R in your diagram.

Note that the robot connector does not provide a 5-volt supply, so you will need to make one from the robot's 10-volt supply.

1.1) Layout

For now, assume that we want c=25 (Volts per Ampere) when converting our current into a voltage.

Lay out your circuit using CMax. To start CMax, run cmax from the command line. Importantly, we will use this circuit as part of a larger design later on, so try to build your circuit using the left-most and right-most 1/3's of the breadboard when laying out your circuit (leaving the center 1/3 open will make it easier to add other components later on).

Because we will eventually power these circuits from the robots, your circuit should use a Robot Connector to provide +10V and ground. These potentials are available on pins 2 and 4 of the robot connector, respectively. Do not use a separate power supply.

Recall that our op-amps are packaged as shown below:

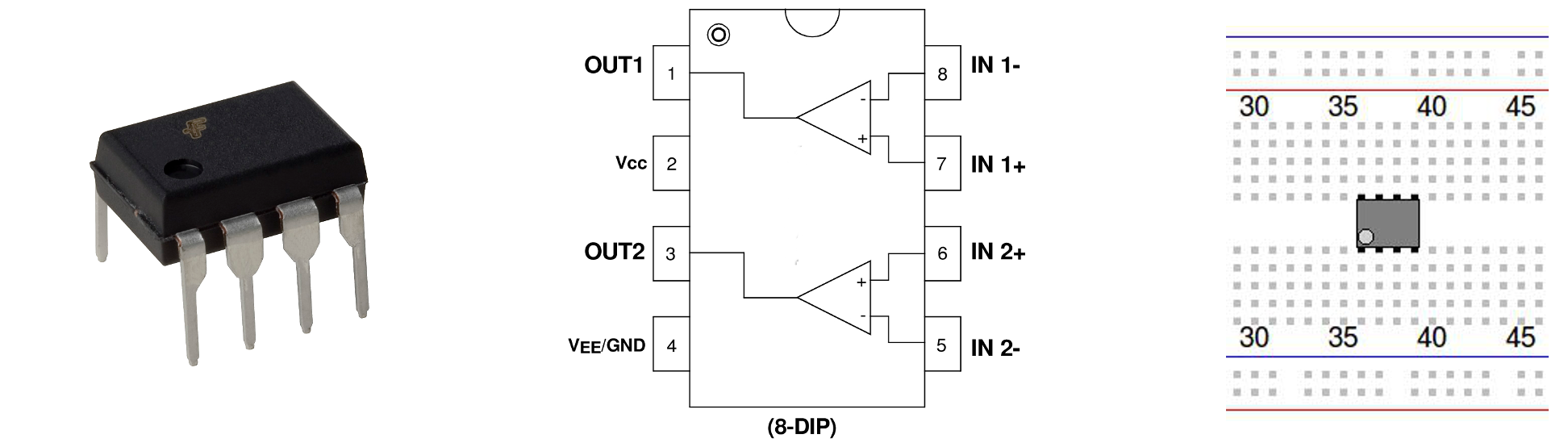
These pinouts are also included on the last page of the handout, which you may remove.

Error on line 4 of question tag.
    csq_display_name = 'CMax: '

ModuleNotFoundError: No module named 'simulate'

1.2) Build It

Now, construct your circuit for measuring both V_L and V_R on a physical protoboard and test it. Note that we do not have 25\Omega resistors available. How could you approximate a 25\Omega resistance using the resistor values we do have?

Even though you are using a voltage divider to create your 5V source, you should not use 25\Omega resistors to construct that divider. You should use resistances around 1k\Omega for that purpose.

Make sure the "eyes" on the head are connected to the base of the head via a silver 6-pin cable:

Use an IR LED keychain to shine some light on the photodetector. Test that your circuit is working by measuring the voltage V_L and V_R when shining an IR light on the eyes from a few different distances. You should see V_L decrease, for example, as the light source moves farther away from the robot.

Check Yourself 2:

Quantitatively, how would you expect the measured voltage to vary with the distance of the light source, if the relationship between the current from the photodetector and the intensity of the light falling on it is linear?

Checkoff 1:
Demonstrate your working circuit to a staff member.

2) Sweep the Light, Johnny

We are interested in how V_L and V_R change as functions of the difference between the light's angle and the head's angle. Henceforth, we will refer to the angular position of the light at \theta_l, and the angular position of the head as \theta_h. Both \theta_l and \theta_h are measured relative to the front of the robot, as shown in the diagram below:

2.1) Setup

In this section, we will run an experiment to try to determine this relationship. We will use soar to help run this experiment. In order to get set up:

1. Turn off the robot.
2. Make sure a black cable connects from the motor to the base of the robot head.
3. Make sure a grey cable connects from the base of the robot head to the card containing the photodetectors.
4. Make sure a red cable connects from the base of the robot head to your protoboard.
5. Connect your circuit so that it is powered from the robot (pins 2 and 4 of the robot connector).
6. Connect V_L to pin 1 of the robot connector so that the robot can measure V_L
7. Connect V_R to pin 3 of the robot connector so that the robot can measure V_R.
8. Connect pin 7 of the head connector (motor +) to pin 6 of the robot connector (analog output).
9. Connect pin 8 of the head connector (motor -) to your 5-volt supply (not the 10V supply of the robot).
10. Turn on the robot.

2.2) Running

Now, to run the experiment, load the dataCollect.py brain into soar. The brain will do the following:

1. The brain will turn the robot head quickly so that it is facing as far counter-clockwise as possible
2. The brain will start recording data about V_L and V_R
3. The brain will slowly turn the robot head clockwise, collecting voltage readings, until the head is turned as far clockwise as possible.

Check Yourself 3:

If you are holding a light straight in front of the robot head and it moves as described above, how would you expect V_L to change as the robot makes its sweep? V_R? V_L - V_R?

Hold an IR light source straight in front of the robot head, about 2 feet away from the head (note that you can use a sheet of paper, which is 11 inches long, to approximate a foot, and so holding the light two "sheet of paper units" away from the head is a good way to approximate 2 feet). Run the brain, and click "stop" once the head has stopped moving.

Check Yourself 4:

The generated plot shows red, green, and blue lines. What does each of these lines represent?

2.3) Running Again

Now, repeat your experiment, but with double the resistance (for example, 50\Omega instead of 25\Omega).

Check Yourself 5:

How do the graphs change as the resistances change? Which of these resistance values makes the best sensor, if our goal is to sense the angle of the light relative to the head?

Checkoff 2:
Discuss the results of your experiments so far, with a staff member.

3) (Infra)Red Rover

We would like to integrate the robot's "eyes" with the motor that turns the head (its "neck"), with the goal of making the head point toward an infrared light source.

3.1) Analysis

Although V_L and V_R sense brightnesses, we can think of their difference as sensing angle, as follows. Let \theta_h represent the angle of the head and \theta_l represent the angle of the light, as in the diagram on the previous page.

Check Yourself 6:

Below, sketch (V_L - V_R) as a function of \theta_l when \theta_h = \frac{\pi}{2} radians.
Hint: at what value of \theta_l should V_L-V_R be zero?

Check Yourself 7:

Sketch (V_L - V_R) as a function of (\theta_l-\theta_h).

Notice that V_L-V_R is proportional to \theta_l-\theta_h when the difference between \theta_l and \theta_h is sufficiently small. We will call the constant of proportionality k_s:

Check Yourself 8:

What are the units of k_s?

How does k_s manifest itself in the graphs above?

3.2) Controller

Because of the geometry of the head and neck, the sensor voltage (V_L-V_R) is appoximately proportional to the difference between the light angle \theta_l and head angle \theta_h. Therefore, we can think about light tracking as a feedback system, where we set a control voltage V_C proportional to the difference between the light angle and the head angle. We will model the motor as taking in this control voltage (representing the voltage drop across the motor) and outputting its angular position in radians. In this diagram, k_c is the gain of the proportional controller:

Check Yourself 9:

Label \theta_h, \theta_l, and V_C in the diagram above. Can you represent V_L and V_R in this diagram?

3.3) Design

Design a circuit to implement this proportional controller. In the space provided in your handout, draw a schematic for this circuit. Include in your schematic the circuitry for generating V_L and V_R from I_L and I_R, as well as the motor (including the connections to both motor terminals). The last sheet of the paper handout includes a listing of op-amp topologies which may be helpful.

Checkoff 3:
Discuss your design, as well as the results of your analysis, with a staff member. How can you adjust k_c in your circuit?

3.4) Layout and Simulation

Use CMax to lay out your light-tracking circuit. As before, use the robot connector to provide power to your circuit. Recall also that the head's motor is connected to pins 7 and 8 of the head connector.

Test your circuit using the dl7_pingpong_1ft.csim simulation file, which alternates the light source between a position to the left of the robot, and a position to the right of the robot, at a fixed distance of 1 foot.

Check Yourself 10:

To what angle is the light being moved in the "ping pong" simulation?

Experiment with different values of k_c to "optimize" the performance of your light tracker.

Check Yourself 11:

Is it possible to adjust k_c so that the tracker oscillates? If so, what is one value of k_c the leads to oscillatory behavior?

Is it possible to adjust k_c so that the tracker diverges? If so, what is one value of k_c that leads to divergent behavior?

Check Yourself 12:

What is the "optimal" value of k_c?

Once you have your circuit working, save the resulting plots.

Also be sure to save your CMax circuit, and to send it to your partner!

Checkoff 4:
Discuss the results of your simulations with a staff member.

4) Appendix: Op-Amp Topologies

4.1) Voltage Follower (Buffer)

\displaystyle{V_o = V_i}

4.2) Non-inverting Amplifier

\displaystyle{V_o = \frac{R_2+R_1}{R_1}V_i}

4.3) Differential Amplifier

\displaystyle{V_o = \frac{R_2}{R_1}(V_2-V_1) + V_3}

5) Appendix: Circuit Part Pin-outs

5.1) Head Connector

5.2) Robot Connector

5.3) Op-Amp (L272A)

¹As we have done throughout the semester, we will use this model to help us reason about the device's behavior. It is important to remember, though, that this is only a model, and is not exactly how the device behaves. (click to return to text)