Files

1) Getting Started

Do this lab with your assigned partner. You and your partner will need a laptop that reliably runs CMax.

You will also need some circuit components, which are available from the front of the room.

Proto Board	Power Supply	Two Clip Leads	Wire Kit
Multimeter	Potentiometer	Six-pin Connector	Lego Motor
Black Motor Cable	L272 Package (Contains 2 Op-Amps)

2) Lego Motor

Over the next few weeks, we'll be adding a new light sensor to our robot. One key piece of this light sensor will be a motor. Ultimately, we'll use this motor to turn our sensor to face a nearby light source. For this lab, though, we'll get started by experimenting with the motor to see how it behaves and how we can control it.

2.1) Motor Resistance

The electrical port of the Lego motor attaches to a 6-pin (6 PIN!!) proto board connector via a short black cable. Notice that the two ends of the cable are different: one fits into the motor and the other fits into the 6-pin connector. The motor is driven by the voltage difference between pins 5 and 6 of the connector. We will not use pins 1-4 in this lab. Do not connect any part of your circuit to those pins.

Connect the Lego motor to a proto board using a 6-pin connector. Use a multimeter to measure the resistance r_ m of the Lego motor. Hint: You can measure resistance by setting the meter to \Omega . You should not be hooked up to the power supply when you measure resistance.

Check Yourself 1:

What is the resistance of the motor?

2.2) Driving the motor

• Adjust the voltage at the $+15$ V output of a power supply to $0 V$, and then turn the power supply off (while you connect the motor).
• Use alligator clip leads with bits of wire to connect $+15$V and **GND** to the power rails of the proto board with the 6-pin motor connector. Wire pins 5 and 6 of the motor connector to the power and ground rails, respectively.
• Use clip leads to connect a multimeter so that you can read the voltage between these pins.
• Turn on the power supply. Slowly increase the power supply voltage, and note the relation between the motor speed and applied voltage.

Check Yourself 2:

What is the minimum voltage required to make the motor turn?

Check Yourself 3:

Swap the connections to power and ground. What happens?

3) Controlling motor speed

We noticed in the previous section that the motor has an angular speed that is proportional to the voltage drop across its terminals.

Our goal is to control the motor electronically. We will ultimately mount the motor on the robot and use the robot's power supply, which is constant at 10V, but we would still like to be able to have a variable voltage drop across the LEGO motor so that we can run it at different speeds. The point of this section is to find a way to use a constant-voltage power supply to get a range of motor speeds.

Return of the Potentiometer

In last week's lab, we used a potentiometer (pot) to create a variable voltage from our 10-volt supply, which we then measured using the robot's analog-to-digital converters (voltage meters). We then used this voltage to steer the robot.

Today, we would like to do roughly the same thing. In this section, we will use a potentiometer to generate a variable voltage, and we will connect that to our motor, in order to try to control the speed of the motor using a potentiometer.

Last week, we used a joystick to turn the robot; the joystick had two potentiometers in it (one that changed as you moved the joystick up and down, and one that changed as you moved the joystick left and right. Today, instead of the joystick, we will use a single, stand-alone potentiometer that comes in a small blue package:

The illustrations below show how these resistors are actually connected inside the potentiometer:

As the angle varies between from \alpha=0 to \alpha=1, the resistance between the middle terminal and each of the two outside terminals will change.

Check Yourself 4:

Use your multimeter to measure the resistance of the pot (R_p). What is this resistance?

Check Yourself 5:

We want to generate a voltage that is directly proportional to \alpha. In order to do so, which terminal of the pot should be connected to 10V, and which should be connected to ground?

Now consider the following circuit, designed to generate a variable voltage across the motor, and thus a variable speed, proportional to \alpha:

3.1) Build It

Reset your power supply to 10V, and build the circuit shown in the schematic above.

Check Yourself 6:

How does the motor's speed change as you change \alpha? Is this what you would expect?

3.2) Theory

Use circuit theory along with modeling the motor as a resistor to estimate, to within 0.5 volts, the voltage across the motor, for the values of \alpha given in the table below. Don't use a spreadsheet or a calculator. Use the resistance you measured earlier and what you learned in last week's labs.

Then find the value of \alpha such that the motor voltage is 5V (one-half of its maximum value), accurate to within 10^{-3}. Hint: Draw the circuit with approximate resistor values, and look for a parallel combination.

What is the voltage V_{motor} (in Volts) when \alpha = 0? 

Approximately what is the voltage V_{motor} (in Volts) when \alpha = 0.5? 

What is the voltage V_{motor} (in Volts) when \alpha = 1?

At approximately what value of \alpha is V_{motor} equal to 5 volts?

Then place these four points approximately on a graph of V_{motor} versus \alpha, and sketch a smooth curve through them.

Check Yourself 7:

Does this curve agree with the results from your physical circuit?

Check Yourself 8:

What would the sketch look like if you had reversed the connections to power and ground on the pot?

Check Yourself 9:

Does the theory explain the behavior you saw in your circuit? If you are unsure about your results so far, please ask a staff member for help before continuing on.

4) Buffering the motor voltage

We can use an operational amplifier to act as a buffer that isolates the voltage divider from the motor. We use L272A operational amplifiers (op amps) that are packaged so that two op amps fit in an 8-pin DIP (Dual-Inline-Package), as shown below.

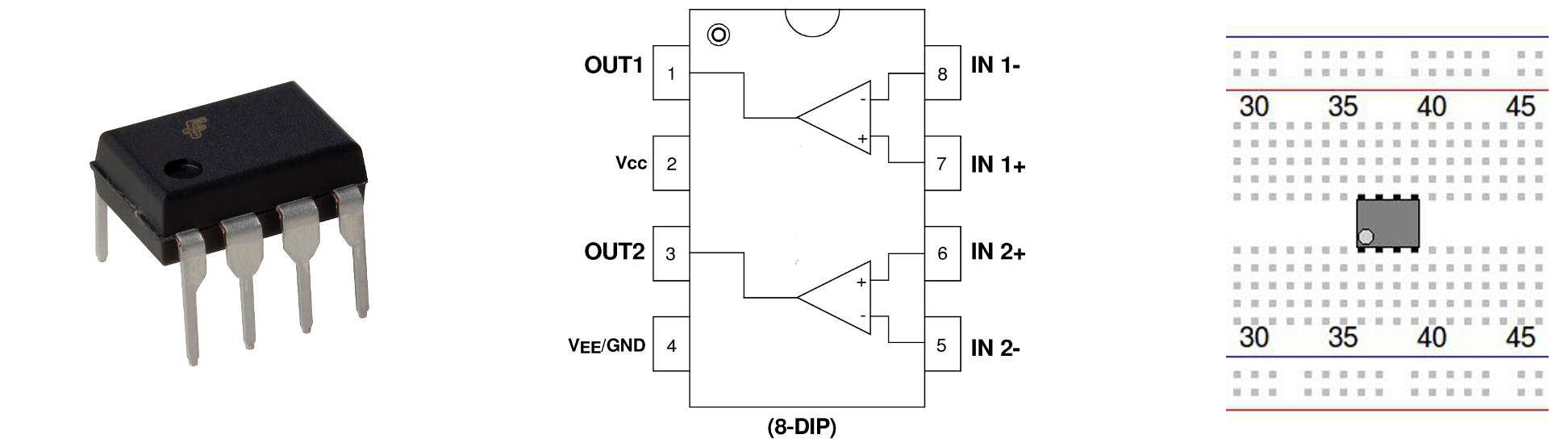
The spacing of the pins is such that the package can be conveniently inserted into a breadboard as shown above (notice that a dot marks pin 1).

A simple "buffer" circuit is shown below. We will learn how to systematically analyze op amp circuits next week. For this week, it is sufficient to understand two basic properties of op amps:

• the currents into the + and - inputs are essentially zero, and

Thus, no current will flow into the + input, and the potentiometer will operate as an unloaded voltage divider. At the same time, the voltage at the output of the op amp will equal the voltage at the + input.

Check Yourself 10:

Notice that the circuit above consists of three distinct pieces:

• the variable voltage divider (made from the pot)
• the buffer (made from the op-amp)
• the motor

Circle each of these pieces in the schematic above.

4.1) Build It

Build the buffered divider circuit on your proto board. Measure the voltage across the motor and observe the motor's behavior as \alpha varies.

Check Yourself 11:

Compare the behaviors of the circuit with and without the buffer. How does the motor's rotational velocity relate to \alpha after the buffer has been added? What properties of the op-amp account for this change?

Checkoff 1:
Explain to a staff member the results of your experiments, with and without buffering.

5) Bidirectional Speed Controller

This circuit allows control of the speed of the motor, but it does not allow us to change the direction the motor turns. To make our robot head turn both left and right, we will need to design a bidirectional speed controller.

The unilateral limitation of the previous circuit results from the fact that our op-amp operates from a single +10V power supply (which is the only power supply available from the robot, which will eventually have to power our "head"). A simple way to adapt our previous controller for bidirectional operation is illustrated below.

The key new component in the bidirectional speed controller is the voltage source V_X.

Check Yourself 12:

What value of V_X gives the most symmetric range of positive and negative speeds for the motor?

Modify the circuit diagram below to show your design. Sketch the resulting circuit diagram in your handout.

Check Yourself 13:

Would a circuit that contains just a voltage divider be sufficient? Explain.

5.1) Layout and Simulation

Use CMax to lay out your bidirectional control circuit. Again, make sure to use only short horizontal or vertical wires, and avoid crossing wires.

Test your circuit with the dl06_pot_signal_steps.csim simulation file from this week's code distribution, which simulates turning the potentiometer first to \alpha = 0.4 and holding it there, then turning it to \alpha = 0.5 and holding it there, and finally turning it to \alpha = 0.6 and holding it there. Notice that this file is also in this week's distribution (type ~ into the File name field to get back to home), rather than in the default location for simulation files.

Check Yourself 14:

We would like for our circuit to make the motor:

• turn in the negative direction when \alpha < 0.5
• stop when \alpha \approx 0.5
• turn in the position direction when \alpha > 0.5
• turn faster as |\alpha - 0.5| gets larger

Looking at the graphs from CMax, does your circuit accomplish these goals?

Paste the code for your CMax circuit below:

Error on line 4 of question tag.
    csq_potAlphaSignal=[float(i)/100. for i in range(101)]

ModuleNotFoundError: No module named 'simulate'

5.2) Build It

Build your bidirectional controller on your proto board. Make your physical circuit look exactly like your CMax layout. Test your circuit to make sure that it behaves as a bidirectional speed controller.

Checkoff 2:
Demonstrate your working simulation and circuit. Explain the relation between motor speed and potentiometer angle, and how your circuit accomplishes bidirectional speed control. Save your plots, as well as your CMax circuit.

6) Fight the Power

So far, we have seen that the speed of the motor goes like the voltage drop across it. Let's do some more experiments to explore this relationship further.

Start by connecting a second motor to a separate breadboard via a 6-pin connector, with nothing else connected to it. Attach a hand-crank to the motor (ask a staff member for one).

Set your multimeter to measure voltages, and measure the voltage drop across the motor (between pins 5 and 6 of the 6-pin connector) as you turn the crank.

Check Yourself 15:

How does the voltage you measure relate to the speed of the motor? What happens if you turn the motor in the opposite direction?

Motors are devices that transform electrical signals to mechanical signals. As we saw before, motors can turn voltages into speeds. But, as we have just seen, motors can also be used as generators, turning mechanical energy into electrical energy (turning speed into voltage).

Check Yourself 16:

How could you model the motor in this setup, using circuit components we've discussed in 6.01?

6.1) Effects of Loading

Now we'll explore what happens when we add an electrical load to our circuit. In this case, we'll use a very small resistor as our load.

Check Yourself 17:

What current would we (theoretically) expect to be flowing through our load resistor if we are turning the motor so that the drop across it is 4V, and our load has a resistance of 0.1\Omega? What if it had a resistance of 0.01\Omega? What about the limit as its resistance goes to 0\Omega?

Start by turning the hand-crank so that the drop across the motor is approximately constant at around 4 volts.

While you are turning the crank, have your partner connect a long wire between pins 5 and 6 of the motor.

Check Yourself 18:

What difference did you feel when turning the motor, with and without the load?

It turns out that our model of a speed-controlled voltage source was not entirely accurate, as we saw in the previous experiment. In actuality, our motor enforces a relationship between electrical and mechanical power.

Electrical power is defined as the product of voltage and current:

And for rotational systems, mechanical power is defined as the product of torque and rotational velocity:

In our system, this means that the power supplied by turning the motor should be about the same as the power required by the load.

Check Yourself 19:

If the generator is producing 4V, what power was required from the generator before adding a load? What power was required with the load added (assume the wire was approximately 0.1\Omega)?

How can you use the above to explain the effect you felt?

6.2) A Different Load

Now let's explore a slightly different load. Grab a second motor (and black cable and 6-pin connector), and connect pins 5 and 6 of the motors together. Here we'll be using one of the motors as a generator, to provide power for the other motor.

Turn the hand-crank on the motor that is providing power. What happens to the other motor?

Something very interesting is happening here. The mechanical power you provide by turning the crank is converted into electrical power by the first motor. Then the second motor turns that electrical power back into mechanical power.

In this case, we have:

Check Yourself 20:

As one partner turns the hand-crank, have the other partner grab the other motor (to change the mechanical power requirements). What difference do you feel when turning the hand-crank when this happens?

How can this be explained in terms of the power in the system?

Check Yourself 21:

As we've seen before, op-amps can isolate pieces of a circuit from one another. If we were to insert a buffer between the two motors, how would this equation change?

6.3) Conflict Resolution

Let's try adding a buffer between the two motors. In this case, because the voltage produced by the generator can be positive or negative, we will have to be a little bit careful about how we connect up the buffer. If you're curious as to why we do this, please ask a staff member for help.

Here is a schematic diagram for this circuit:

Check Yourself 22:

Repeat your experiment from above (having one partner grab the rotor of the second motor while the other turns the crank). How is the effect different from before? Can you explain this in terms of power?

6.4) Crank-powered Servo Motor

Finally, connect your servo motor from checkoff 2 so that, rather than being powered from the bench supply, it is powered by your generator (but you should still be able to change the speed/direction of the motor using the potentiometer on the breadboard).

Checkoff 3:
Discuss the results of your experiments with a staff member.

7) Clean Up